Ever tried to approximate a complex function using a Taylor polynomial? If so, you’ve probably wondered just how accurate that estimate is. That’s where the Lagrange Error Bound comes in. It helps us figure out the maximum possible error when we use a Taylor polynomial.
Don’t worry! This may sound complicated, but it’s really not. Let’s break it down in a fun and simple way.
What Is the Lagrange Error Bound?
Imagine you want to estimate the value of a function, like ex or sin(x). You use a Taylor polynomial to do this. But hey—as great as Taylor polynomials are, they’re not perfect.
The Lagrange Error Bound tells you how much your approximation might be off. It’s like checking how much you might overshoot or undershoot your target.
The formula looks like this:
Rn(x) = (f(n+1)(c) × (x – a)n+1) / (n+1)!
Yeah, that looks intense, but let’s decode it.
- f(n+1)(c) means the (n+1)th derivative of the function, evaluated at some point c between a and x.
- (x – a)n+1 is the difference between your input and the center, raised to the power of n+1.
- (n+1)! is just the factorial of (n+1)—multiply all numbers from 1 to n+1.
Basically, this formula bounds the error. It says, “Your real error won’t be bigger than this.”
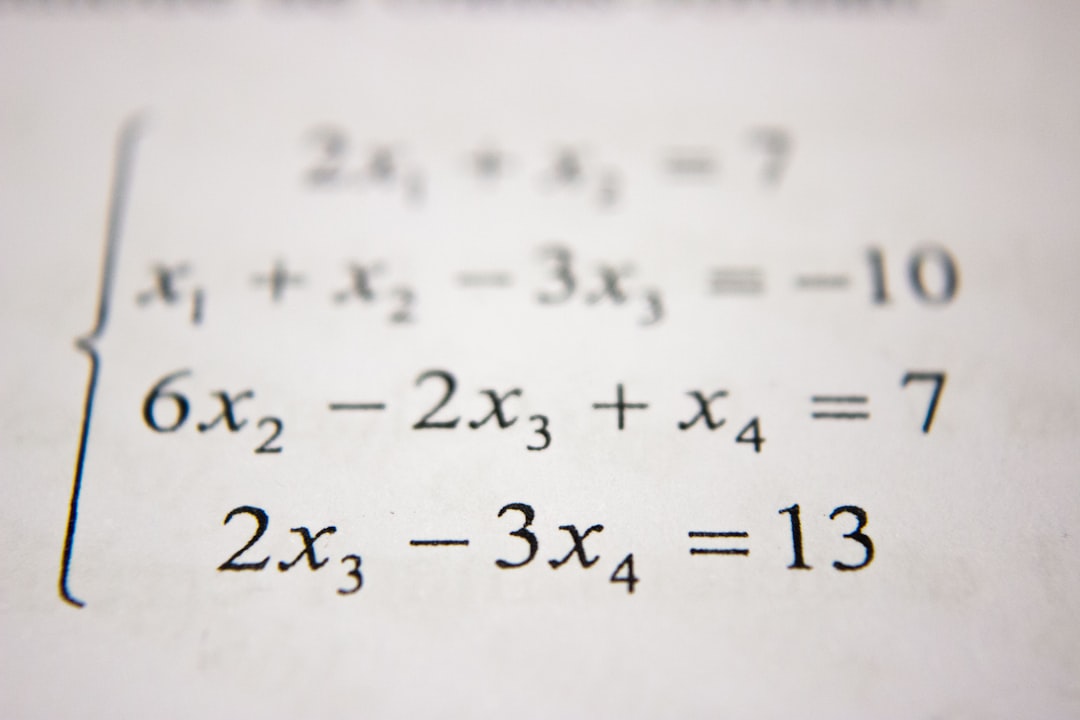
Why Does It Matter?
Engineers, scientists, coders—they all need to make approximations. They also need to know how close those estimates are.
Using Lagrange Error Bound helps you:
- Improve your approximations
- Control how much error is acceptable
- Decide how many terms (n) you need in your polynomial
Fun Fact: You don’t always have to find the exact value of c. If you can estimate the maximum value of the derivative on that interval, you’re good!
Cool Example!
Wanna estimate e0.5 using a second-degree Taylor polynomial centered at 0?
We write the Taylor polynomial for ex:
P2(x) = 1 + x + (x2/2!)
So, P2(0.5) = 1 + 0.5 + (0.52 / 2) = 1.625
But how close is that to the real value of e0.5?
Let’s use the error bound! The third derivative of ex is still ex. And the max value between 0 and 0.5 is e0.5 ≈ 1.65.
Error ≤ (1.65 × (0.5)3) / 3! = (1.65 × 0.125)/6 ≈ 0.0344
This means the real value of e0.5 is within 0.0344 of 1.625!
Top Tips to Use It Easily
- Choose a near your x. Closer means smaller error.
- Pick an n high enough to make the error tiny.
- If your function’s derivatives are wild, check that max value carefully!
Real Life Uses
You’ll find Lagrange Error Bound working behind the scenes in:
- Physics: Velocity and acceleration approximations
- Computer Graphics: Rendering curves and shapes
- Robotics: Controlling movement with polynomial paths
- Finance: Estimating growth using exponential functions
Pretty cool, right?
Remember This!
The Lagrange Error Bound lets you play with polynomials confidently. It tells you, “Hey, this estimate is close enough for what you need.”
So next time you use a Taylor polynomial, be sure to bring this powerful little tool along!
Math isn’t just about numbers—it’s about knowing just how far off you might be!